作者:解学武
分块查找算法完全攻略(原理、实现及时间复杂度)
一般对于需要查找的待查数据元素列表来说,如果很少变化或者几乎不变,则我们完全可以通过排序把这个列表排好序以便我们以后查找。但是对于经常增加数据元素的列表来说,要是每次增加数据都排序的话,那真的是有点太累人了。
所以之前我们分析过,对于几乎不变的数据列表来说,排序之后使用二分查找是很不错的,但是对于经常变动的数据元素列表来说,每次排序后再使用二分查找则不是很好的选择。
分块查找是结合二分查找和顺序查找的一种改进方法。在分块查找里有索引表和分块的概念。索引表就是帮助分块查找的一个分块依据,其实就是一个数组,用来存储每块的最大存储值,也就是范围上限;分块就是通过索引表把数据分为几块。
在每需要增加一个元素的时候,我们就需要首先根据索引表,知道这个数据应该在哪一块,然后直接把这个数据加到相应的块里面,而块内的元素之间本身不需要有序。因为块内无须有序,所以分块查找特别适合元素经常动态变化的情况。
分块查找只需要索引表有序,当索引表比较大的时候,可以对索引表进行二分查找,锁定块的位置,然后对块内的元素使用顺序查找。这样的总体性能虽然不会比二分查找好,却比顺序查找好很多,最重要的是不需要数列完全有序。
如图 1 所示是一个已经分好块的数据,同时有个索引表,现在我们要在数据中插入一个元素,该怎么做呢?
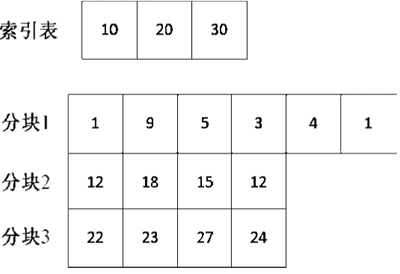
图 1 分块的插入
首先,我们看到索引表是 10、20、30,对于元素 15 来说,应该将其放在分块 2 中。于是,分块 2 的数据变为 12、18、15、12、15,直接把 15 插入分块 2 的最后就好了。
接下来是查找操作。如果要查找图 1 中的 27 这个数,则首先该怎么做呢?通过二分查找索引表,我们发现 27 在分块 3 里,然后在分块 3 中顺序查找,得到 27 存在于数列中。
现在分块查找的操作步骤很明了,我们接下来写一下分块查找的代码实现:
分块查找由于只需要索引表有序,所以特别适合用于在动态变化的数据元素序列中查找。但是如何分块比较复杂。如果分块过于稀疏,则可能导致每一块的内容过多,在顺序查找时效率很低;如果分块过密,则又会导致块数很多,无论是插入还是删除数据,都会频繁地进行二分查找;如果块数特别多,则基本上和直接二分查找的动态插入数据类似,这样分块查找就没有意义了。
所以对于分块查找来说,可以根据数据量的大小及数据的区间来进行对分块的选择。二分查找的平均查找长度近似 log2(n+1)-1,这里的n是块数;顺序查找的平均查找长度为 (n+1)/2,这里的 n 是每块的个数。
尽量等分为固定的块,假设块数为 a,每个块内的元素数量为 b,则 b=n/a,那么接下来就好办了,如果给定一个数据量 n 进行分块,则总的平均查找长度为 (b+1)/2+log2(a+1)-1,这样就可以解出 a 和 b 分别为多少了。
分块查找有点类似于哈希表,但又不如散列表好用,其实很多时候我们在编程中并不会直接用到这个算法,但是分块的思想在很多时候还是很有用的。
但是我们经常用到汇总表。举个例子,我们要统计一个视频网站中每个用户的观看行为,即每个用户分别观看每个视频多长时间。这个记录量很大。怎么处理呢?如果把每一个这样的记录都记录到一个表里,那就真的太恐怖了,一天可能有几千万的量,统计的时间长一些,通过数据库就查不出来了。
于是我们一般会根据具体的业务量做分表。可能一天一个表,具体的表名可能是 t_user_watch_xxx_20160211,表示这张表是 2016 年 2 月 11 日的记录表。在做存储和查询的时候就可以按照时间去做一个表的分块,再查询详细的记录了。其实这里用到的就是分块的思想。
声明:当前文章为本站“玩转C语言和数据结构”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
所以之前我们分析过,对于几乎不变的数据列表来说,排序之后使用二分查找是很不错的,但是对于经常变动的数据元素列表来说,每次排序后再使用二分查找则不是很好的选择。
什么是分块查找
由于上面所提到的,对于需要经常增加或减少数据的数据元素列表,我们每次增加或减少数据之后排序,或者每次查找前排序都不是很好的选择,这样无疑会增加查找的复杂度,在这种情况下可以采用分块查找。分块查找是结合二分查找和顺序查找的一种改进方法。在分块查找里有索引表和分块的概念。索引表就是帮助分块查找的一个分块依据,其实就是一个数组,用来存储每块的最大存储值,也就是范围上限;分块就是通过索引表把数据分为几块。
在每需要增加一个元素的时候,我们就需要首先根据索引表,知道这个数据应该在哪一块,然后直接把这个数据加到相应的块里面,而块内的元素之间本身不需要有序。因为块内无须有序,所以分块查找特别适合元素经常动态变化的情况。
分块查找只需要索引表有序,当索引表比较大的时候,可以对索引表进行二分查找,锁定块的位置,然后对块内的元素使用顺序查找。这样的总体性能虽然不会比二分查找好,却比顺序查找好很多,最重要的是不需要数列完全有序。
分块查找的原理及实现
分块查找要求把一个数据分为若干块,每一块里面的元素可以是无序的,但是块与块之间的元素需要是有序的。对于一个非递减的数列来说,第i块中的每个元素一定比第i-1块中的任意元素大。同时,分块查找需要一个索引表,用来限定每一块的范围。在增加、删除、查找元素时都需要用到。如图 1 所示是一个已经分好块的数据,同时有个索引表,现在我们要在数据中插入一个元素,该怎么做呢?

图 1 分块的插入
首先,我们看到索引表是 10、20、30,对于元素 15 来说,应该将其放在分块 2 中。于是,分块 2 的数据变为 12、18、15、12、15,直接把 15 插入分块 2 的最后就好了。
接下来是查找操作。如果要查找图 1 中的 27 这个数,则首先该怎么做呢?通过二分查找索引表,我们发现 27 在分块 3 里,然后在分块 3 中顺序查找,得到 27 存在于数列中。
现在分块查找的操作步骤很明了,我们接下来写一下分块查找的代码实现:
import me.irfen.algorithm.ch01.ArrayList;
public class BlockSearch {
private int[] index;
private ArrayList[] list;
/**
* 初始化索引表
* @param index
*/
public BlockSearch(int[] index) {
if (index != null && index.length != 0) {
this.index = index;
this.list = new ArrayList[index.length];
for (int i = 0; i < list.length; i++) {
list[i] = new ArrayList();
}
} else {
throw new Error("index cannot be null or empty.");
}
}
/**
* 插入元素
* @param value
*/
public void insert(int value) {
int i = binarySearch(value);
list[i].add(value);
}
/**
* 查找元素
* @param data
* @return
*/
public boolean search(int data) {
int i = binarySearch(data);
for (int j = 0; j < list[i].size(); j++) {
if (data == list[i].get(j)) {
return true;
}
}
return false;
}
/**
* 打印每块元素
*/
public void printAll() {
for (int i = 0; i < list.length; i++) {
ArrayList l = list[i];
System.out.println("ArrayList " + i + ":");
for (int j = 0; j < l.size(); j++) {
System.out.println(l.get(j));
}
}
}
/**
* 二分查找定位索引位置
* @param data 要插入的值
* @return
*/
private int binarySearch(int data) {
int start = 0;
int end = index.length;
int mid = -1;
while (start <= end) {
mid = (start + end) / 2;
if (index[mid] > data) {
end = mid - 1;
} else {
// 如果相等,也插入在后面
start = mid + 1;
}
}
return start;
}
}
下面是测试代码,用来检验查找的正确性:
public class BlockSearchTest {
public static void main(String[] args) {
int[] index = {10, 20, 30};
BlockSearch blockSearch = new BlockSearch(index);
blockSearch.insert(1);
blockSearch.insert(12);
blockSearch.insert(22);
blockSearch.insert(9);
blockSearch.insert(18);
blockSearch.insert(23);
blockSearch.insert(5);
blockSearch.insert(15);
blockSearch.insert(27);
blockSearch.printAll();
System.out.println(blockSearch.search(18));
System.out.println(blockSearch.search(29));
}
}
分块查找的特点与性能分析
分块查找的特点其实显而易见,那就是分块查找拥有顺序查找和二分查找的双重优势,即顺序查找不需要有序,二分查找的速度快。分块查找由于只需要索引表有序,所以特别适合用于在动态变化的数据元素序列中查找。但是如何分块比较复杂。如果分块过于稀疏,则可能导致每一块的内容过多,在顺序查找时效率很低;如果分块过密,则又会导致块数很多,无论是插入还是删除数据,都会频繁地进行二分查找;如果块数特别多,则基本上和直接二分查找的动态插入数据类似,这样分块查找就没有意义了。
所以对于分块查找来说,可以根据数据量的大小及数据的区间来进行对分块的选择。二分查找的平均查找长度近似 log2(n+1)-1,这里的n是块数;顺序查找的平均查找长度为 (n+1)/2,这里的 n 是每块的个数。
尽量等分为固定的块,假设块数为 a,每个块内的元素数量为 b,则 b=n/a,那么接下来就好办了,如果给定一个数据量 n 进行分块,则总的平均查找长度为 (b+1)/2+log2(a+1)-1,这样就可以解出 a 和 b 分别为多少了。
分块查找的适用场景
其实分块查找有很多可用之处。一个现实场景就是,有些年级在有大型考试的时候,都是随机分配每个人的考试座位的,交考试卷的时候试卷上的名字、班级是有封条的,一个年级的所有试卷最终是一些老师一起改的。在得出最终分数之后,才拆开所有的封条,按照班级来分配试卷。这里的“按照班级”也就是分块。分块查找有点类似于哈希表,但又不如散列表好用,其实很多时候我们在编程中并不会直接用到这个算法,但是分块的思想在很多时候还是很有用的。
但是我们经常用到汇总表。举个例子,我们要统计一个视频网站中每个用户的观看行为,即每个用户分别观看每个视频多长时间。这个记录量很大。怎么处理呢?如果把每一个这样的记录都记录到一个表里,那就真的太恐怖了,一天可能有几千万的量,统计的时间长一些,通过数据库就查不出来了。
于是我们一般会根据具体的业务量做分表。可能一天一个表,具体的表名可能是 t_user_watch_xxx_20160211,表示这张表是 2016 年 2 月 11 日的记录表。在做存储和查询的时候就可以按照时间去做一个表的分块,再查询详细的记录了。其实这里用到的就是分块的思想。
声明:当前文章为本站“玩转C语言和数据结构”官方原创,由国家机构和地方版权局所签发的权威证书所保护。



 ICP备案:
ICP备案: 公安部网络备案:
公安部网络备案: